معادلة شرودنغر - Schrödinger equation

ما هي معادلة شرودنغر الموجية – Schrödinger equation؟

معادلة شرودنغر، التي تسمى أحياناً معادلة شرودنجر الموجية، هي معادلة تفاضلية جزئية. يستخدم مفهوم الحفاظ على الطاقة (الطاقة الحركية + الطاقة الكامنة = الطاقة الإجمالية) للحصول على معلومات حول سلوك الإلكترون المرتبط بالنواة. يقوم بذلك عن طريق السماح بحساب دالة الموجة للإلكترون (Ψ).

حل معادلة شرودنغر يعطينا (Ψ و2Ψ). مع هذه نحصل على الأرقام الكمومية وأشكال واتجاهات المدارات التي تميز الإلكترونات في الذرة أو الجزيء. تقدم معادلة “شرودنغر” حلولاً دقيقة فقط للنواة ذات إلكترون واحد. في اللغة الرياضية، نقول أنّ الحلول التحليلية لـ (Ψ) ممكنة فقط لأنظمة الإلكترون الواحد. غالباً ما توصف أنظمة الإلكترون الواحد بأنّها هيدروجينية، بمعنى أي أنّها “مثل الهيدروجين”.

بالنسبة لجميع الذرات والأيونات والجزيئات الأخرى، لا توجد حلول تحليلية لـ (Ψ)، ثم يتم استخدام طرق الحساب التقريبية، مثل نظرية التقريب المداري والتغير. هناك معادلة “شرودنغر” تعتمد على الوقت ومعادلة “شرودنغر” المستقلة عن الوقت. تعتبر المعادلة المستقلة عن الوقت أنّ الحالة الكمومية للإلكترون لا تتغير، ومن ثم فهي تعتبر الإلكترون موجة ثابتة.

تسمح المعادلة المستقلة عن الوقت بإيجاد كثافة الإلكترون (أي أحجام وأشكال المدارات الذرية والجزيئية) باستخدام (Ψ2)، مربع الدالة الموجية.

شرح معادلة شرودنغر:

معادلة “شرودنغر”، هي المعادلة الأساسية لعلم الظواهر تحت المجهرية المعروفة باسم ميكانيكا الكم. المعادلة، التي طورها الفيزيائي النمساوي “إروين شرودنغر” (1926م)، لها نفس الأهمية المركزية لميكانيكا الكم مثل قوانين نيوتن للحركة للظواهر واسعة النطاق للميكانيكا الكلاسيكية.

معادلة الموجة بشكل أساسي، تصف معادلة “شرودنغر” شكل الموجات الاحتمالية أو “وظائف الموجة” التي تحكم حركة الجسيمات الصغيرة، وتحدد كيفية تغيير هذه الموجات من خلال التأثيرات الخارجية. أسس “شرودنغر” صحة المعادلة من خلال تطبيقها على ذرة الهيدروجين، وتوقع العديد من خصائصها بدقة ملحوظة. تُستخدم المعادلة على نطاق واسع في فيزياء الذرة والنووية والفيزياء الصلبة.

أنواع معادلة شرودنغر:

معادلة شرودنغر المستقلة عن الزمن:

يمكن التعبير عن معادلة “شرودنغر” المستقلة عن الزمن باختصار رياضي مضغوط للغاية على النحو التالي:

Η ψ = Ε ψ

تنطبق المعادلة على الإلكترونات التي تنتقل بسرعات غير نسبية. (هذا يعني أنّه يتطلب تعديلات قبل أن يتم تطبيقه على عناصر كتلة عالية)، المعادلة تقول:

“مجموع الطاقة الحركية والطاقة الكامنة لوظيفة الموجة = الطاقة الكلية لوظيفة الموجة”.

يمكن كتابة المعادلة المستقلة عن الوقت في أي نظام إحداثيات مناسب، مثل الإحداثيات الديكارتية (x ،y ،z)، بالنسبة للذرات الهيدروجينية، تكون الإحداثيات القطبية الكروية أكثر ملاءمة، ومن ثم:

(- h² / 2m ) ∇² ψ (r) + V (r) ψ (r) = E Ψ (r)

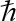– هو انخفاض ثابت بلانك.

m – هي كتلة الإلكترون.

– هو مشغل (Laplacian).

Ψ – هي وظيفة الموجة.

V  – هي الطاقة الكامنة.

E – هي القيمة الذاتية للطاقة.

(r) – يدل على أنّ الكميات هي وظائف الإحداثيات القطبية الكروية (r ،θ ،φ).

القيود التي تؤدي إلى التكميم:

تم حل المعادلة لإيجاد (Ψ). القيود المفروضة على حل المعادلة تنتج تكميماً، أي أنّ الحلول الموجودة لـ (Ψ) تقتصر على قيم معينة وجميع القيم الأخرى ممنوعة.

هذه القيود هي:

• (Ψ) ومشتقاتها الجزئية الأولى يجب أن تكون مستمرة.

• (Ψ) يجب أن تكون قابلة للتطبيع: هذا يعني أنّ هناك احتمالاً بنسبة (100٪) لوجود الإلكترون في مكان ما في الكون. للحصول على قيمة حقيقية، يتطلب التطبيع ما يلي:

∫ ψ² dr = 1 

• مع زيادة المسافة من النواة، ينفصل الإلكترون ولا يعد مقيداً. مثل (r → ∞ ، H → +H + – e).

كيف تنتج الدالة الموجية أرقام كمومية؟

توجد الدالة الموجية للإلكترون في ثلاثة أبعاد، لذلك تتكون حلول معادلة “شرودنغر” من ثلاثة أجزاء. يتم الحصول عليها صراحة من خلال طريقة حل المعادلات التفاضلية الجزئية تسمى “فصل المتغيرات”. عند القيام بذلك، نحصل على:

Ψ(r, θ, φ) = R(r) P(θ) F(φ)

اتضح أن حلول ممكنة فقط ل (Ψ) عندما:

• في (R (r، ثابت نسميه (n)، له قيم (1 ، 2 ، 3 ، 4 ، ….).

• في (P (θ، ثابت نسميه (l)، له قيم (0 ، 1 ، 2 ، 3 ، … (n-1)).

• في (F (φ، ثابت ، نسميه (ml)، له قيم (-l ،(l + 1) ،… 0 … ،(l + 1) ، l).

وهكذا من دالة الموجة، أعطت معادلة “شرودنغر” الأرقام الكمية الثلاثة التي تميز سلوك الإلكترون في الذرة:

• n – هو الرقم الكمي الرئيسي.

• l – العدد الكمي للزخم الزاوي المداري.

• ml – رقم الكم المغناطيسي.