طريقة تحليل الشبكة الفائقة Super Mesh Circuit Analysis

ما هو تحليل الشبكة الفائقة Super Mesh Circuit Analysis؟

بدلاً من استخدام تحليل الشبكة (mesh analysis)، لتحليل الشبكة الكهربائية المعقدة، يعد (Super Mesh) أو (Super Mesh Analysis) أسلوبًا جيدًا، حيث يكون هناك مصدر تيار للتجريد كعنصر مشترك. هذا هو المكان الذي نستخدم فيه تحليل دائرة الملاحظات الفائقة بدلاً من تحليل العقدة (node) أو الدائرة العقدية (nodal circuit analysis).

لتبسيط مثل هذه الشبكة حيث يتم تعيين العقدة الفائقة (super node)، عن طريق إغلاق مصدر الجهد بالكامل داخل العقدة الفائقة وتقليل عدد العقد المرجعية بمقدار واحد (1) لكل منها. يكون مصدر الجهد. في تقنية تحليل الشبكة الفائقة، يكون مصدر التيار في المجال الداخلي للشبكة الفائقة. لذلك، نحن قادرون على تقليل عدد الشبكات بمقدار واحد (1) لكل مصدر تيار موجود في الدائرة الكهربائية.

إذا كان من الممكن تجاهل شبكة واحدة، إذا كان مصدر التيار الكهربائي “في تلك الشبكة” على محيط الدائرة الكهربائية. بدلاً من ذلك، ينطبق قانون كيرشوف الثاني للجهد(KVL) “قانون الجهد في (Kirchhoff)” فقط على تلك الشبكات أو الشبكة الفائقة في الدائرة المتجددة. من الصعب فهم التمهيد، لذلك سنحل أولاً دائرة بسيطة من خلال تحليل دائرة الشبكة الفائقة، وبعد ذلك، سنلخص تحليل الشبكة الفائقة الكامل (خطوة بخطوة).

مثال لشرح تحليل الشبكة الفائقة Super Mesh Circuit Analysis:

استخدم تحليل الشبكة الفائقة (Super Mesh) للعثور على الجهد (V3) والتيارات (Current i1) و(i2) و(i3) في الشكل التالي:

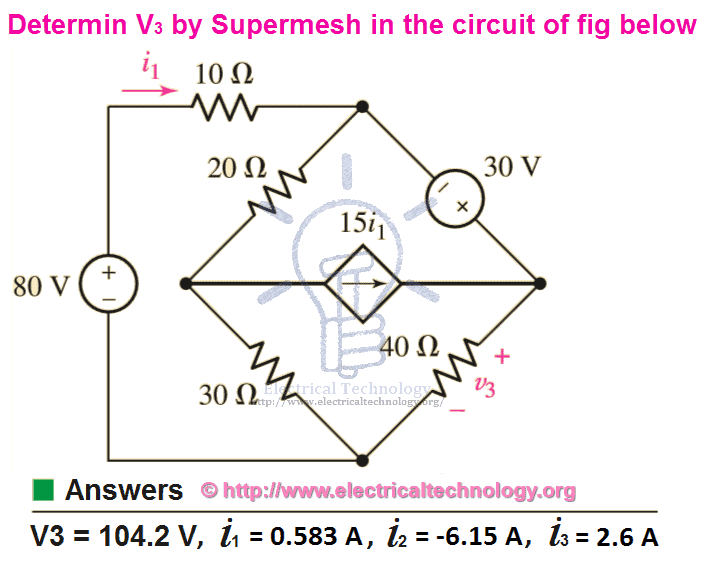
الحل: 

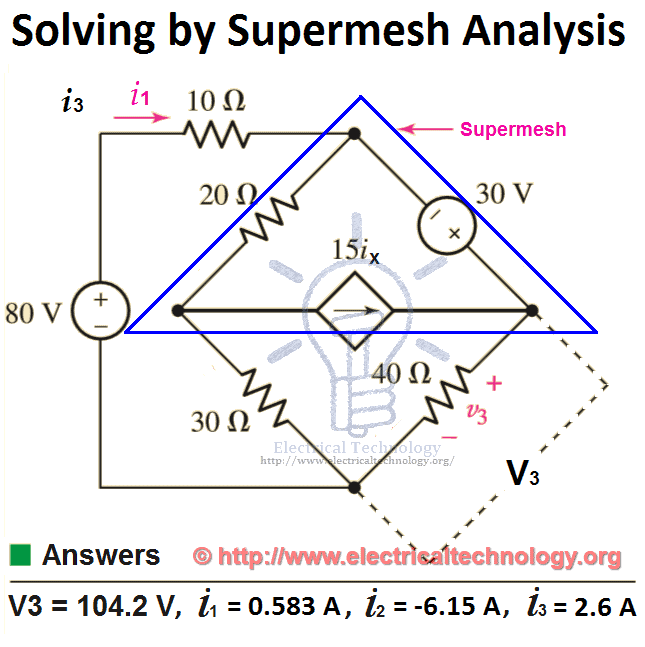
استخدام (KVL) على شبكة (1):

80 = 10i₁ + 20(i₁–i₂) + 30 (i₁–i₃)

بالتبسيط:

80 = 10i₁ + 20i₁ -20i₂ + 30i₁-30i₃

80 = 60i₁ – 20i₂ – 30i₃ ….. → Eq 1

قم الآن بتطبيق قانون كيرشوف للجهد (KVL) على (Supermesh)، “وهو تكامل بين (mesh 2) و(mesh 3)، لكننا قللناها بشبكة واحدة تُعرف باسم (supermesh):

30 = 40i₃ + 30(i₃–i₁) +20(i₂–i₁)

30 = 40i₃ + 30i₃ – 30i₁ +20i₂-20i₁

30 = 70i₃ – 50i₁ +20i₂ ….. → Eq 2

لكن لدينا هنا ثلاثة (3) متغيرات، وهي (i1) و(i2) و(i3). وهناك معادلتان. لذلك نحتاج إلى ثلاث معادلات أيضًا. يرتبط مصدر التيار المستقل “في الشبكة الفائقة” بتيارات الشبكة المفترضة، أي:

15ix = i₃–i₂

I3=15ix+i₂ ….. → Eq 3

حل المعادلات (1) و(2) و(3) من خلال قاعدة كريمر (Cramer’s rule) أو حاسبة قاعدة كريمر (Cramer’s rule calculator) أو الحذف أو حذف غاوس (Gauss Elimination) أو برنامج بمساعدة الكمبيوتر مثل (MATLAB)، نجد:

i₁ = 0.583 A

i₂ = -6.15 A

i₃ = 2.6 A

يمكننا أيضًا إيجاد قيمة (v3):

V₃ = i₃ x R₃

بوضع القيم:

V₃ = 2.6A x 40Ω

V₃ = 104 V

ملخص تحليل الشبكة الفائقة خطوة بخطوة:

• قم بتقييم ما إذا كانت الدائرة عبارة عن دائرة مستوية. إذا كانت الإجابة بنعم، فقم بتطبيق (Supermesh). إذا كانت الإجابة لا، فقم بإجراء تحليل عقدي بدلاً من ذلك.

• أعد رسم الدائرة إذا لزم الأمر وعد عدد الشبكات في الدائرة.

• قم بتسمية كل من التيارات الشبكية في الدائرة. كقاعدة عامة، يؤدي تحديد جميع التيارات الشبكية للتدفق في اتجاه عقارب الساعة إلى تحليل دائرة أبسط.

• شكّل شبكة فائقة إذا كانت الدائرة تحتوي على مصادر تيار بواسطة شبكتين. لذلك، فإنّ الشبكة الفائقة ستحيط كلا الشبكتين.

• اكتب (KVL)، “قانون الجهد في (Kirchoff)” حول كل شبكة وشبكة فائقة في الدائرة. تبدأ مع عقدة واحدة سهلة وسوف يتم تركيبها. تابع الآن في اتجاه شبكة التيار. خذ علامة “-” في الحساب أثناء كتابة معادلات (KVL) وحل الدائرة. لا حاجة إلى معادلة (KVL) إذا كان مصدر التيار يقع على محيط الشبكة. لذلك، يتم تحديد تيار الشبكة وتقييمه عن طريق الفحص.

• هناك حاجة إلى (KCL) واحد، “قانون (Kirchhoff) الأول للتيار، لكل شبكة فائقة محددة ويمكن تحقيقها عن طريق تطبيق بسيط لـ (KCL). بكلمات بسيطة، اربط التيار المتدفق من كل مصدر تيار بتيارات الشبكة.

• يمكن أن تحدث حالة إضافية إذا كانت الدائرة تحتوي على مصادر أخرى تابعة. في هذه الحالة، قم بالتعبير عن أي قيم إضافية غير معروفة و(qantitis) مثل التيارات (ir) الفولتية بخلاف التيارات الشبكية من حيث التيارات الشبكية المناسبة.

• رتب ونظم نظام المعادلات.

• أخيرًا، حل نظام المعادلات للجهود العقدية (Nodal voltages)، مثل (V1) و(V2) و(V3) وما إلى ذلك، سيكون هناك (Mesh) منهم. إذا وجدت صعوبات في حل نظام المعادلات، فارجع إلى المثال أعلاه.